Background
After learning about Delta, Gamma, and Theta, we’re ready to dive into one of the most intriguing Options Greeks: Vega. Vega, as most of you may have surmised, is the rate of change of option premium in relation to volatility change. But the question is, what exactly is volatility? I’ve asked several traders this topic, and the most popular response is “Volatility is the up-and-down movement of the stock market.” If you share my views on volatility, it is past time we addressed this.
So here’s the plan; I’m guessing this will take several chapters –
- We will understand what volatility really means
- Understand how to measure volatility
- Practical Application of volatility
- Understand different types of volatility
- Understand Vega
So let’s get started.
Moneyball
Have you seen the Hollywood movie ‘Moneyball’? Billy Beane is the manager of a baseball team in the United States, and this is a true story. The film follows Billy Beane and his young colleague as they use statistics to uncover relatively unknown but exceptionally brilliant baseball players. A method unheard of at the time, and one that proved to be both inventive and revolutionary.
Moneyball’s trailer may be viewed here.
I enjoy this film not just because of Brad Pitt, but also because of the message it conveys about life and business. I won’t go into specifics right now, but let me draw some inspiration from the Moneyball technique to assist illustrate volatility:).
Please don’t be dismayed if the topic below appears irrelevant to financial markets. I can tell you that it is important and will help you better understand the phrase “volatility.”
Consider two batsmen and the number of runs they have scored in six straight matches –
| Match | Billy | Mike |
|---|
| 1 | 20 | 45 |
| 2 | 23 | 13 |
| 3 | 21 | 18 |
| 4 | 24 | 12 |
| 5 | 19 | 26 |
| 6 | 23 | 19 |
You are the team’s captain, and you must select either Billy or Mike for the seventh match. The batsman should be trustworthy in the sense that he or she should be able to score at least 20 runs. Who would you pick? According to my observations, people address this topic in one of two ways:
- Calculate both batsman’s total score (also known as ‘Sigma’) and select the batsman with the highest score for the following game. Or…
- Calculate the average (also known as ‘Mean’) amount of runs scored per game and select the hitter with the higher average.
Let us do the same and see what results we obtain –
- Billy’s Sigma = 20 + 23 + 21 + 24 + 19 + 23 = 130
- Mike’s Sigma = 45 + 13 + 18 + 12 + 26 + 19 = 133
So, based on the sigma, you should go with Mike. Let us compute the mean or average for both players and see who performs better –
- Billy = 130/6 = 21.67
- Mike = 133/6 = 22.16
Mike appears to be deserving of selection based on both the mean and the sigma. But don’t jump to any conclusions just yet. Remember, the goal is to select a player who can score at least 20 runs, and with the information we currently have (mean and sigma), there is no way to determine who can score at least 20 runs. As a result, let us conduct additional research.
To begin, we will compute the deviation from the mean for each match played. For example, we know Billy’s mean is 21.67 and that he scored 20 runs in his first encounter. As a result, the departure from the mean from the first match is 20 – 21.67 = – 1.67. In other words, he scored 1.67 runs below his average. It was 23 – 21.67 = +1.33 during the second match, which means he scored 1.33 runs more than his usual score.
Here is a diagram that represents the same thing (for Billy) –
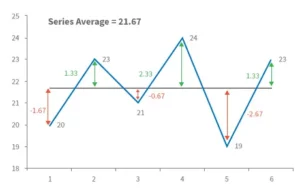
For each match played, the middle black line indicates Billy’s average score, while the double arrowed vertical line reflects his deviation from the norm. We shall now calculate another variable named ‘Variance.’
The sum of the squares of the deviation divided by the total number of observations is the definition of variance. This may appear to be frightening, but it is not. We know that the total number of observations in this situation is equal to the total number of matches played, so 6.
As a result, the variance may be computed as –
Variance = [(-1.67) ^2 + (1.33) ^2 + (-0.67) ^2 + (+2.33) ^2 + (-2.67) ^2 + (1.33) ^2] / 6
= 19.33 / 6
= 3.22
Further, we will define another variable called ‘Standard Deviation’ (SD) which is calculated as –
std deviation = √ variance
So the standard deviation for Billy is –
= SQRT (3.22)
= 1.79
Similarly, Mike’s standard deviation equals 11.18.
Let’s add up all of the figures (or statistics) –
| Statistics | Billy | Mike |
|---|
| Sigma | 130 | 133 |
| Mean | 21.6 | 22.16 |
| SD | 1.79 | 11.18 |
We understand what ‘Mean’ and ‘Sigma’ mean, but what about SD? The standard deviation represents the difference from the mean.
The textbook definition of SD is as follows: “The standard deviation (SD, also denoted by the Greek letter sigma, ) is a metric used in statistics to quantify the amount of variation or dispersion of a set of data values.”
Please do not mistake the two sigmas – the total is also known as sigma represented by the Greek symbol, and the standard deviation is also known as sigma represented by the Greek symbol.
| Player | Lower Estimate | Upper Estimate |
|---|
| Billy | 21.6 – 1.79 = 19.81 | 21.6 + 1.79 = 23.39 |
| Mike | 22.16 – 11.18 = 10.98 | 22.16 + 11.18 = 33.34 |
These figures indicate that in the upcoming 7th match, Billy is likely to score between 19.81 and 23.39, while Mike is likely to score between 10.98 and 33.34. Mike’s range makes it difficult to predict whether he will score at least 20 runs. He can score 10, 34, or anything in between.
Billy, on the other hand, appears to be more consistent. His range is limited, thus he will neither be a power hitter nor a bad player. He is predicted to be consistent and should score between 19 and 23 points. In other words, picking Mike over Billy for the seventh match can be dangerous.
Returning to our initial question, who do you believe is most likely to score at least 20 runs? The answer must be obvious by now; it must be Billy. In comparison to Mike, Billy is more consistent and less hazardous.
So, in general, we used “Standard Deviation” to estimate the riskiness of these players. As a result, ‘Standard Deviation’ must indicate ‘Risk.’ In the stock market, volatility is defined as the riskiness of a stock or index. Volatility is expressed as a percentage and is calculated using the standard deviation.
Volatility is defined as “a statistical measure of the dispersion of returns for certain security or market index” by Investopedia. Volatility can be measured using either the standard deviation or the variance of returns from the same securities or market index. The bigger the standard deviation, the greater the risk.”
According to the aforementioned criterion, if Infosys and TCS have volatility of 25% and 45 percent, respectively, then Infosys has less dangerous price swings than TCS.
Some food for thought
Before I wrap this chapter, let’s make some predictions –
Today’s Date = 15th July 2015
Nifty Spot = 8547
Nifty Volatility = 16.5%
TCS Spot = 2585
TCS Volatility = 27%
Given this knowledge, can you forecast the anticipated trading range for Nifty and TCS one year from now?
Of course, we can, so let’s put the math to work –
| Asset | Lower Estimate | Upper Estimate |
|---|
| Nifty | 8547 – (16.5% * 8547) = 7136 | 8547 + (16.5% * 8547) = 9957 |
| TCS | 2585 – (27% * 2585) = 1887 | 2585 + (27% * 2585) = 3282 |
So, based on the aforementioned calculations, Nifty is expected to trade between 7136 and 9957 in the next year, with all values in between having a varied likelihood of occurrence. This suggests that on July 15, 2016, the probability of the Nifty being around 7500 is 25%, while the probability of it being around 8600 is 40%.
This brings us to a fascinating platform –
- We estimated the Nifty range for a year; can we estimate the range Nifty is expected to trade in the next few days or the range Nifty is likely to trade up till the series expiry?
- If we can accomplish this, we will be in a better position to identify options that are likely to expire worthless, which means we can sell them now and pocket the premiums.
- We estimated that the Nifty will trade between 7136 and 9957 in the next year, but how certain are we? Is there any level of certainty in expressing this range?
- How is Volatility calculated? I know we talked about it previously in the chapter, but is there a simpler way? We could use Microsoft Excel!
- We computed the Nifty’s range using a volatility estimate of 16.5 percent; what if the volatility changes?
We’ll answer all of these topics and more in the next chapters!
Calculating Volatility in Excel
In the previous chapter, we discussed the notion of standard deviation and how it may be used to assess a stock’s ‘Risk or Volatility.’ Before we go any further, I’d like to discuss how volatility can be calculated. Volatility data is not easily accessible, therefore knowing how to compute it yourself is always a smart idea.
Of course, we looked at this calculation in the previous chapter (recall the Billy & Mike example), and we outlined the procedures as follows –
- Determine the average
- Subtract the average from the actual observation to calculate the variance.
- Variance is calculated by squaring and adding all deviations.
- Determine the standard deviation by taking the square root of the variance.
The goal of doing this in the previous chapter was to demonstrate the mechanics of standard deviation calculation. In my opinion, it is critical to understand what goes beyond a formula because it just increases your thoughts. However, in this chapter, we will use MS Excel to compute the standard deviation or volatility of a specific stock. MS Excel follows the identical processes as described previously, but with the addition of a button click.
I’ll start with the border steps and then go over each one in detail –
- Download historical closing price data.
- Determine the daily returns.
- Make use of the STDEV function.
So let us get started right now.
Step 1 – Download the historical closing prices
This may be done with any data source you have. The NSE India website and Yahoo Finance are two free and dependable data providers.
For the time being, I shall use data from the NSE India. At this point, I must tell you that the NSE’s website is pretty informative, and I believe it is one of the top stock exchange websites in the world in terms of information supplied.
Here is a snapshot where I have highlighted the search option –
Once you have this, simply click on ‘Download file in CSV format (highlighted in the green box) and you’re done.
You now have the necessary data in Excel. Of course, in addition to the closing prices, you have a wealth of other information. I normally remove any unnecessary information and only keep the date and closing price. This gives the sheet a clean, crisp appearance.
Here’s a screenshot of my excel sheet at this point –
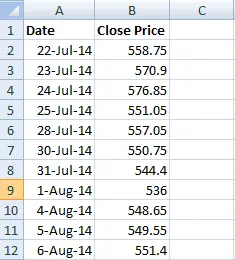
Please keep in mind that I have removed all extraneous material. I only kept the date and the closing prices.
Step 2 – Calculate Daily Returns
We know that the daily returns can be calculated as –
Return = (Ending Price / Beginning Price) – 1
However, for all practical purposes and ease of calculation, this equation can be approximated to:
Return = LN (Ending Price / Beginning Price), where LN denotes Logarithm to Base ‘e’, note this is also called ‘Log Returns’.
Here is a snapshot showing you how I’ve calculated the daily log returns of WIPRO –
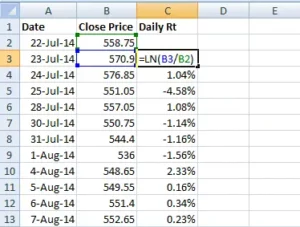
To calculate the lengthy returns, I utilized the Excel function ‘LN’.
Step 3 – Use the STDEV Function
After calculating the daily returns, you may use an excel function called ‘STDEV’ to calculate the standard deviation of daily returns, which is the daily volatility of WIPRO.
Note – In order to use the STDEV function all you need to do is this –
- Take the cursor an empty cell
- Press ‘=’
- Follow the = sign by the function syntax i.e STDEV and open a bracket, hence the empty cell would look like =STEDEV(
- After the open bracket, select all the daily return data points and close the bracket
- Press enter
Here is the snapshot which shows the same –
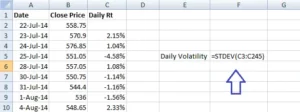
Once this is completed, Excel will quickly determine WIPRO’s daily standard deviation, often known as volatility. I receive 0.0147 as the answer, which when converted to a percentage equals 1.47 percent.
This means that WIPRO’s daily volatility is 1.47 percent!
WIPRO’s daily volatility has been estimated, but what about its annual volatility?
Now here’s a crucial rule to remember: to convert daily volatility to annual volatility, simply multiply the daily volatility value by the square root of time.
Similarly, to convert annual volatility to daily volatility, divide it by the square root of time.
So, we’ve estimated the daily volatility in this situation, and now we need WIPRO’s annual volatility. We’ll do the same thing here –
- Daily Volatility = 1.47%
- Time = 252
- Annual Volatility = 1.47% * SQRT (252)
- = 23.33%
In fact, I have calculated the same in excel, have a look at the image below –
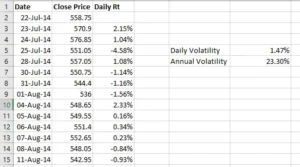
As a result, we know that WIPRO’s daily volatility is 1.47 percent and its annual volatility is approximately 23 percent.
Let’s compare these figures to what the NSE has published on its website. The NSE only discloses these figures for F&O stocks and not for other stocks. Here is a screenshot of the same –
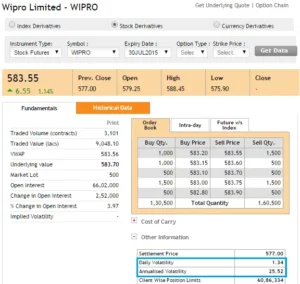
Our figure is very close to what the NSE has computed – according to the NSE, Wipro’s daily volatility is roughly 1.34 percent and its annualized volatility is about 25.5 percent.
So, what’s the deal with the minor discrepancy between our calculation and NSEs? – One probable explanation is that we use spot prices while the NSE uses futures prices. However, I’m not interested in delving into why this minor discrepancy exists. The goal here is to understand how to calculate the volatility of a security based on its daily returns.
Let us conduct one more calculation before we finish this chapter. If we know the annual volatility of WIPRO is 25.5 percent, how can we calculate its daily volatility?
As previously stated, to convert yearly volatility to daily volatility, simply divide the annual volatility by the square root of time, resulting in –
= 25.5% / SQRT (252)
= 1.60%
So far, we’ve learned what volatility is and how to calculate it. The practical use of volatility will be discussed in the following chapter.
Remember that we are still learning about volatility; however, the ultimate goal is to comprehend what the options Greek Vega signifies. Please don’t lose sight of our ultimate goal.
Background
We discussed previously the range within which the Nifty is likely to move given its yearly volatility. We estimated an upper and lower end range for Nifty and decided that it is likely to move inside that range.
Okay, but how certain are we about this? Is it possible that the Nifty will trade outside of this range? If so, what is the likelihood that it will trade outside of the range, and what is the likelihood that it will trade within the range? What are the values of the outside range if one exists?
Finding answers to these issues is critical for a number of reasons. If nothing else, it will create the groundwork for a quantitative approach to markets that is considerably distinct from the traditional fundamental and technical analysis thought processes.
So let us delve a little deeper to get our solutions.
Random Walk
The discussion that is about to begin is extremely important and highly pertinent to the matter at hand, as well as extremely interesting.
Consider the image below –
What you’re looking at is known as a ‘Galton Board.’ A Galton Board is a board with pins adhered to it. Collecting bins are located directly behind these pins.
The goal is to drop a little ball above the pins. When you drop the ball, it hits the first pin, after which it can either turn left or right before hitting another pin. The same method is repeated until the ball falls into one of the bins below.
Please keep in mind that once you drop the ball from the top, you will be unable to control its route until it lands in one of the bins. The ball’s course is fully spontaneous and not planned or regulated. Because of this, the path that the ball takes is known as the ‘Random Walk.’
Can you image what would happen if you dropped dozens of these balls one after the other? Each ball will obviously take a random walk before falling into one of the containers. What are your thoughts on the distribution of these balls in the bins?
- Will they all be grouped together? or
- Will they be spread evenly across the bins? or
- Will they fall into the various bins at random?
People who are unfamiliar with this experiment may be tempted to believe that the balls fall randomly across numerous bins and do not follow any particular pattern. But this does not occur; there appears to order here.
Consider the image below –
When you drop multiple balls on the Galton Board, each one taking a random walk, they all appear to be dispersed in the same way –
- The majority of the balls end up in the middle bin.
- There are fewer balls as you travel away from the middle bin (to the left or right).
- There are very few balls in the bins at the extreme ends.
This type of distribution is known as the “Normal Distribution.” You may have heard of the bell curve in school; it is nothing more than the normal distribution. The best aspect is that no matter how many times you perform this experiment, the balls will always be spread in a normal distribution.
This is a highly popular experiment known as the Galton Board experiment; I strongly advise you to watch this wonderful video to better comprehend this debate –
So, why are we talking about the Galton Board experiment and the Normal Distribution?
In reality, many things follow this natural sequence. As an example,
Collect a group of adults and weigh them – Separate the weights into bins (call them weight bins) such as 40kgs to 50kgs, 50kgs to 60kgs, 60kgs to 70kgs, and so on. Counting the number of people in each bin yields a normal distribution.
- If you repeat the experiment with people’s heights, you will get a normal distribution.
- With people’s shoe sizes, you’ll get a Normal Distribution.
- Fruit and vegetable weight
- Commute time on a specific route
- Lifetime of batteries
This list might go on and on, but I’d want to direct your attention to one more fascinating variable that follows the normal distribution – a stock’s daily returns!
The daily returns of a stock or an index cannot be forecast, which means that if you ask me what the return on TCS will be tomorrow, I will be unable to tell you; this is more akin to the random walk that the ball takes. However, if I collect the daily returns of the stock over a specific time period and examine the distribution of these returns, I can see a normal distribution, also known as the bell curve!
To emphasise this point, I plotted the distribution of daily returns for the following stocks/indices –
- Nifty (index)
- Bank Nifty ( index)
- TCS (large cap)
- Cipla (large cap)
- Kitex Garments (small cap)
- Astral Poly (small cap)
Normal Distribution
I believe the following explanation may be a little daunting for someone who is learning about normal distribution for the first time. So here’s what I’ll do: I’ll explain the concept of normal distribution, apply it to the Galton board experiment, and then extrapolate it to the stock market. I hope this helps you understand the gist better.
So, in addition to the Normal Distribution, different distributions can be used to distribute data. Different data sets are distributed statistically in different ways. Other data distribution patterns include binomial distribution, uniform distribution, Poisson distribution, chi-square distribution, and so on. Among the other distributions, the normal distribution pattern is arguably the most extensively studied and researched.
The normal distribution contains a number of qualities that aid in the development of insights into the data set. The normal distribution curve can be fully defined by two numbers: the mean (average) and standard deviation of the distribution.
The mean is the core value in which the highest values are clustered. This is the distribution’s average value. In the Galton board experiment, for example, the mean is the bin with the most balls in it.
So, if I number the bins from left to right as 1, 2, 3…all the way up to 9, the 5th bin (indicated by a red arrow) is the ‘average’ bin. Using the average bin as a guide, the data is distributed on either side of the average reference value. The standard deviation measures how the data is spread out (also known as dispersion) (recollect this also happens to be the volatility in the stock market context).
Here’s something you should know: when someone mentions ‘Standard Deviation (SD),’ they’re usually referring to the first SD. Similarly, there is a second standard deviation (2SD), a third standard deviation (SD), and so on. So when I say SD, I’m just referring to the standard deviation value; 2SD would be twice the SD value, 3SD would be three times the SD value, and so on.
Assume that in the Galton Board experiment, the SD is 1 and the average is 5. Then,
- 1 SD would encompass bins between 4th bin (5 – 1 ) and 6th bin (5 + 1). This is 1 bin to the left and 1 bin to the right of the average bin
- 2 SD would encompass bins between 3rd bin (5 – 2*1) and 7th bin (5 + 2*1)
- 3 SD would encompass bins between 2nd bin (5 – 3*1) and 8th bin (5 + 3*1)
Keeping the preceding in mind, below is the broad theory surrounding the normal distribution that you should be familiar with –
- Within the 1st standard deviation,
- one can observe 68% of the data
- Within the 2nd standard deviation, one can observe 95% of the data
- Within the 3rd standard deviation, one can observe 99.7% of the data
The following image should help you visualize the above –
Using this to apply to the Galton board experiment –
- We can see that 68 percent of balls are collected within the first standard deviation, or between the fourth and sixth bins.
- We can see that 95 percent of balls are collected within the 2nd standard deviation, or between the 3rd and 7th bins.
- Within the third standard deviation, or between the second and eighth bins, 99.7 percent of balls are gathered.
Keeping the above in mind, imagine you are ready to drop a ball on the Galton board and we are both having a chat –
You – I’m about to throw a ball; can you guess which bin it will land in?
Me – No, I can’t since each ball moves at random. However, I can guess the range of bins it could fall into.
Can you forecast the range?
Me – I believe the ball will land between the fourth and sixth bins.
You – How certain are you about this?
Me- I’m 68 percent certain it’ll fall somewhere between the fourth and sixth bins.
You – Well, 68 percent accuracy is a little low; can you predict the range with higher precision?
Me – Of course. I’m 95 percent certain that the ball will land in the third and seventh bins. If you want even more precision, I’d say the ball is most likely to land between the second and eighth bins, and I’m 99.5 percent certain of this.
You – Does it mean the ball has no chance of landing in the first or tenth bin?
Me – Well, there is a potential that the ball will land in one of the bins outside the third SD bins, but it is quite unlikely.
You – How low?
Me – The chances are about as slim as seeing a ‘Black Swan’ in a river. In terms of probability, the possibility is less than 0.5 percent.
You – Tell me more about the Black Swan
Me – Black Swan ‘events,’ as they are known, are events with a low likelihood of occurrence (such as the ball landing in the first or tenth bin). However, one should be aware that black swan events have a non-zero probability and can occur – when and how is difficult to anticipate. The image below depicts the occurrence of a black swan event –
There are many balls dropped in the above image, yet only a few of them collect at the extreme ends.
Normal Distribution and stock returns
Hopefully, the above explanation provided you with a brief overview of the normal distribution. The reason we’re discussing normal distribution is that the daily returns of stocks/indices also form a bell curve or a normal distribution. This suggests that if we know the mean and standard deviation of the stock return, we can have a better understanding of the stock’s return behaviour or dispersion. Let us examine the case of Nifty for the purposes of this debate.
To begin, the distribution of Nifty daily returns is as follows:
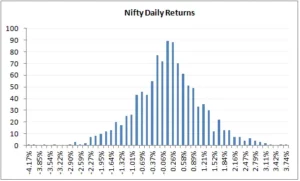
The daily returns, as we can see, are plainly distributed normally. For this distribution, I computed the average and standard deviation (in case you are wondering how to calculate the same, please do refer to the previous chapter). Remember that in order to get these figures, we must first compute the log daily returns.
- Daily Average / Mean = 0.04%
- Daily Standard Deviation / Volatility = 1.046%
- The current market price of Nifty = 8337
Take note that an average of 0.04 percent shows that the nifty’s daily returns are concentrated at 0.04 percent. Now, keeping this knowledge in mind, let us compute the following:
- The range within which Nifty is likely to trade in the next 1 year
- The range within which Nifty is likely to trade over the next 30 days.
We will use 1 and 2 standard deviations meaning with 68 and 95 percent confidence for the computations above.
Solution 1 – (Nifty’s range for the next 1 year)
Average = 0.04%
SD = 1.046%
Let us convert this to annualized numbers –
Average = 0.04*252 = 9.66%
SD = 1.046% * Sqrt (252) = 16.61%
So with 68% confidence, I can say that the value of Nifty is likely to be in the range of –
= Average + 1 SD (Upper Range) and Average – 1 SD (Lower Range)
= 9.66% + 16.61% = 26.66%
= 9.66% – 16.61% = -6.95%
Because we computed this on log daily returns, these percent are log percentages, therefore we need to convert them back to regular percent, which we can do straight and get the range number (in relation to Nifty’s CMP of 8337) –
Upper Range
= 8337 *exponential (26.66%)
= 10841
And for lower range –
= 8337 * exponential (-6.95%)
= 7777
According to the foregoing forecast, the Nifty will most likely trade between 7777 and 10841. How certain am I about this? – As you know, I’m 68 percent certain about this.
Let’s raise the confidence level to 95% or the 2nd standard deviation and see what we get –
Average + 2 SD (Upper Range) and Average – 2 SD (Lower Range)
= 9.66% + 2* 16.61% = 42.87%
= 9.66% – 2* 16.61% = -23.56%
Hence the range works out to –
Upper Range
= 8337 *exponential (42.87%)
= 12800
And for lower range –
= 8337 * exponential
(-23.56%)
= 6587
The following computation implies that, with 95 percent certainty, the Nifty will move between 6587 and 12800 over the next year. Also, as you can see, when we seek higher accuracy, the range expands significantly.
I’d recommend repeating the task with 99.7 percent confidence or 3SD and seeing what kind of range figures you obtain.
Now, supposing you calculate Nifty’s range at 3SD level and get the lower range value of Nifty as 5000 (I’m just stating this as a placeholder number here), does this mean Nifty cannot go below 5000? It absolutely can, but the chances of it falling below 5000 are slim, and if it does, it will be considered a black swan occurrence. You can make the same case for the top end of the range.
Solution 2 – (Nifty’s range for next 30 days)
We know the daily mean and SD –
Average = 0.04%
SD = 1.046%
Because we want to calculate the range for the next 30 days, we must convert it for the appropriate time period –
Average = 0.04% * 30 = 1.15%
SD = 1.046% * sqrt (30) =
5.73%
So I can state with 68 percent certainty that the value of the Nifty during the next 30 days will be in the range of –
= Average + 1 SD (Upper Range) and Average – 1 SD (Lower Range)
= 1.15% + 5.73% = 6.88%
= 1.15% – 5.73% = – 4.58%
Because these are log percentages, we must convert them to ordinary percentages; we can do so right away and get the range value (in respect to the Nifty’s CMP of 8337) –
= 8337 *exponential (6.88%)
= 8930
And for lower range –
= 8337 * exponential (-4.58%)
= 7963
With a 68 percent confidence level, the above computation implies that Nifty will trade between 8930 and 7963 in the next 30 days.
Let’s raise the confidence level to 95% or the 2nd standard deviation and see what we get –
Average + 2 SD (Upper Range) and Average – 2 SD (Lower Range)
= 1.15% + 2* 5.73% = 12.61%
= 1.15% – 2* 5.73% = -10.31%
Hence the range works out to –
= 8337 *exponential (12.61%)
= 9457 (Upper Range)
And for lower range –
= 8337 * exponential (-10.31%)
= 7520
I hope the calculations above are clear to you. You may also download the MS Excel spreadsheet that I used to perform these computations.
Of course, you have a legitimate point at this point – normal distribution is fine – but how do I receive the information to trade? As a result, I believe this chapter is sufficiently long to accept further notions. As a result, we’ll transfer the application section to the next chapter. In the following chapter, we will look at the applications of standard deviation (volatility) and how they relate to trading. In the following chapter, we will go over two crucial topics: (1) how to choose strikes that can be sold/written using normal distribution and (2) how to set up stoploss using volatility.
Striking it right
The previous chapters have provided a basic understanding of volatility, standard deviation, normal distribution, and so on. We will now apply this knowledge to a few practical trading applications. At this point, I’d want to examine two such applications:
- Choosing the best strike to short/write
- Calculating a trade’s stop loss
However, at a much later stage (in a separate module), we will investigate the applications under a new topic – ‘Relative value Arbitrage (Pair Trading) and Volatility Arbitrage’. For the time being, we will only trade options and futures.
So let’s get this party started.
One of the most difficult problems for an option writer is choosing the right strike so that he may write the option, collect the premium, and not be concerned about the potential of the spot shifting against him. Of course, the risk of spot moving against the option writer will always present, but a careful trader can mitigate this risk.
Normal Distribution assists the trader in reducing this concern and increasing his confidence while writing options.
Let us quickly review –
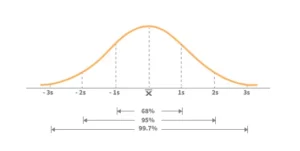
According to the bell curve above, with reference to the mean (average) value –
- 68 percent of the data is clustered around the mean within the first SD, implying that the data has a 68 percent chance of being within the first SD.
- 95 percent of the data is clustered around the mean within the 2nd SD, which means that the data has a 95 percent chance of being within the 2nd SD.
- 99.7 percent of the data is clustered around the mean inside the third standard deviation, which means that there is a 99.7 percent chance that the data is within the third standard deviation.
Because we know that Nifty’s daily returns are typically distributed, the qualities listed above apply to Nifty. So, what does this all mean?
This means that if we know Nifty’s mean and standard deviation, we can make a ‘informed guess’ about the range in which Nifty is expected to move throughout the chosen time frame. Consider the following:
- Date = 11th August 2015
- Number of days for expiry = 16
- Nifty current market price = 8462
- Daily Average Return = 0.04%
- Annualized Return = 14.8%
- Daily SD = 0.89%
- Annualized SD = 17.04%
Given this, I’d like to identify the range within which Nifty will trade till expiry, which is in 16 days –
16 day SD = Daily SD *SQRT (16)
= 0.89% * SQRT (16)
= 3.567%
16 day average = Daily Avg * 16
= 0.04% * 16 = 0.65%
These numbers will help us calculate the upper and lower range within which Nifty is likely to trade over the next 16 days –
Upper Range = 16 day Average + 16 day SD
= 0.65% + 3.567%
= 4.215%, to get the upper range number –
= 8462 * (1+4.215%)
= 8818
Lower Range = 16 day Average – 16 day SD
= 0.65% – 3.567%
= 2.920% to get the lower range number –
= 8462 * (1 – 2.920%)
= 8214
According to the calculations, the Nifty will most likely trade between 8214 and 8818. How certain are we about this? We know that there is a 68 percent chance that this computation will work in our favour. In other words, there is a 32% possibility that the Nifty will trade outside of the 8214-8818 range. This also implies that any strikes outside of the predicted range may be useless.
Hence –
- Because all call options over 8818 are expected to expire worthlessly, you can sell them and receive the premiums.
- Because they are likely to expire worthlessly, you can sell all put options below 8214 and receive the premiums.
Alternatively, if you were considering purchasing Call options above 8818 or Put options below 8214, you should reconsider because you now know that there is a very small possibility that these options would expire in the money, therefore it makes sense to avoid purchasing these strikes.
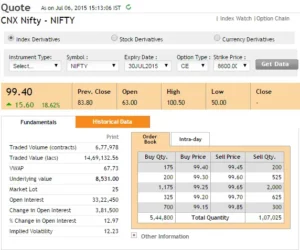
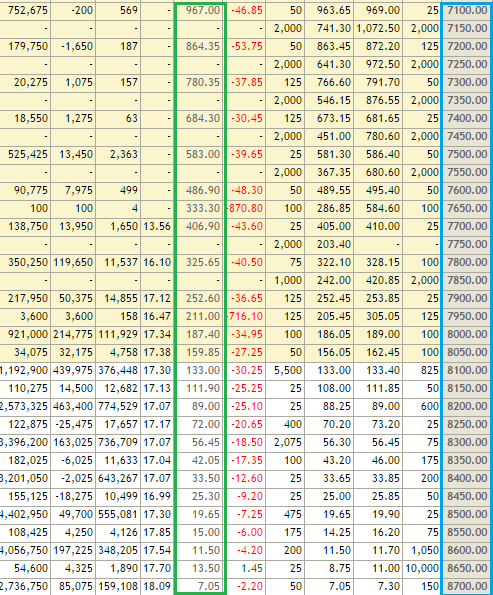
Here is a list of all Nifty Call option strikes above 8818 on which you can write (short) and get premiums –
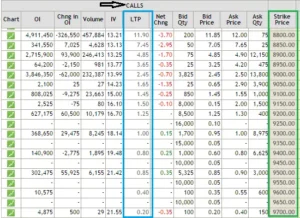
If I had to choose a strike today, it would be either 8850 or 8900, or possibly both, for a premium of Rs.7.45 and Rs.4.85 respectively. The reason I chose these strikes is straightforward: I saw a fair balance of danger (1 SD away) and return (7.45 or 4.85 per lot).
I’m sure many of you have had this thought: if I write the 8850 Call option and earn Rs.7.45 as premium, it doesn’t really translate to anything useful. After all, at Rs.7.45 for each lot, that works out to –
= 7.45 * 25 (lot size)
= Rs.186.25
This is precisely where many traders lose the plot. Many people I know consider gains and losses in terms of absolute value rather than return on investment.
Consider this: the margin required to enter this trade is approximate Rs.12,000/-. If you are unsure about the margin need, I recommend using Zerodha’s margin calculator.
The premium of Rs.186.25/- on a margin deposit of Rs.12,000/- comes out to a return of 1.55 percent, which is not a terrible return by any stretch of the imagination, especially for a 16-day holding period! If you can regularly achieve this every month, you may earn a return of more than 18% annualized solely through option writing.
I use this method to develop options and would like to share some of my ideas on it –
Put Options – I don’t like to short PUT options since panic spreads faster than greed. If there is market panic, the market can tumble considerably faster than you would think. As a result, even before you realise it, the OTM option you wrote may soon become ATM or ITM. As a result, it is preferable to avoid than to regret.
Call Options – If you reverse the preceding statement, you will realise why writing call options is preferable to writing put options. In the Nifty example above, for the 8900 CE to become ATM or ITM, the Nifty must move 438 points in 16 days. This requires excessive greed in the market…and as I previously stated, a 438 up move takes slightly longer than a 438 down move. As a result, I prefer to short solely call options.
Strike identification – I perform the entire operation of identifying the strike (SD, mean calculation, translating the same in relation to the number of days to expiry, picking the appropriate strike just the week before expiry and not earlier). The timing is deliberate.
Timing – I only sell options on the last Friday before the expiry week. Given that the August 2015 series expiry is on the 27th, I’d short the call option only on the 21st of August, around the closing. Why am I doing this? This is mostly to make sure theta works in my advantage. Remember the ‘time decay’ graph from the theta chapter? The graph clearly shows that when we approach expiry, theta kicks in full force.
Premium Collected – Because I write call options so close to expiration, the premiums are always cheap. On the Nifty Index, the premium I get is roughly Rs.5 or 6, equating to a 1.0 percent return. But, for two reasons, I find the trade rather reassuring. (1) To have the trade operate against me (2) Theta works in my favour because premiums erode significantly faster during the last week of expiry, which benefits the option seller.
– Why bother? Most of you may be thinking, “With premiums this low, why should I bother?” To be honest, I had the same impression at first, however over time I understood that deals with the following criteria make sense to me –
- Risk and reward should be visible and quantifiable.
- If a transaction is profitable today, I should be able to reproduce it tomorrow.
- Consistency in identifying opportunities
- Worst-case scenario analysis
This technique meets all of the criteria listed above, hence it is my preferred option.
SD consideration – When I’m writing options 3-4 days before expiry, I prefer to write one SD away, but when I’m writing options much earlier, I prefer to go two SD away. Remember that the greater the SD consideration, the better your confidence level, but the lesser the premium you can receive. Also, as a general rule, I never write options that expire in more than 15 days.
Events – I avoid writing options when there are significant market events such as monetary policy, policy decisions, company announcements, and so on. This is due to the fact that markets tend to respond swiftly to events, and so there is a considerable probability of being caught on the wrong side. As a result, it is preferable to be safe than sorry.
Black Swan – I’m fully aware that, despite my best efforts, markets can shift against me and I could find myself on the wrong side. The cost of being caught on the wrong side, especially in this transaction, is high. Assume you receive 5 or 6 points as a premium but are caught on the wrong side and must pay 15 or 20 points or more. So you gave away all of the tiny gains you made over the previous 9 to 10 months in one month. In fact, the famous Satyajit Das describes option writing as “eating like a bird but pooping like an elephant” in his extremely incisive book “Traders, Guns, and Money.”
The only way to ensure that you limit the impact of a black swan occurrence is to be fully aware that it can occur at any point after you write the option. So, if you decide to pursue this technique, my recommendation is to keep an eye on the markets and evaluate market sentiment at all times. Exit the deal as soon as you see something is incorrect.
Option writing puts you on the edge of your seat in terms of success ratio. There are moments when it appears that markets are working against you (fear of a black swan), but this only lasts a short time. Such roller coaster sentiments are unavoidable when writing options. The worst aspect is that you may be forced to believe that the market is going against you (false signal) and hence exit a potentially profitable trade during this roller coaster ride.
In addition, I exit the transaction when the option moves from OTM to ATM.
Expenses – The key to these trades is to minimise your expenses to a minimal minimum in order to keep as much profit as possible for yourself. Brokerage and other fees are included in the costs. If you sell one lot of Nifty options and get Rs.7 as a premium, you will have to give up a few points as profit. If you trade with Zerodha, your cost per lot will be about 1.95. The greater the number of lots, the lower your cost. So, if I traded 10 lots (with Zerodha) instead of one, my expense drops to 0.3 points. To find out more, try Zerodha’s brokerage calculator.
The cost varies from broker to broker, so be sure your broker is not being greedy by charging you exorbitant brokerage fees. Even better, if you are not already a member of Zerodha, now is the moment to join us and become a part of our wonderful family.
Allocation of Capital – At this point, you may be wondering, “How much money do I put into this trade?” Do I put all of my money at danger or only a portion of it? How much would it be if it’s a percentage? Because there is no simple answer, I’ll use this opportunity to reveal my asset allocation strategy.
Because I am a firm believer in equities as an asset class, I cannot invest in gold, fixed deposits, or real estate. My whole money (savings) is invested in equities and equity-related items. Any individual should, however, diversify their capital across several asset types.
So, within Equity, here’s how I divided my money:
- My money is invested in equity-based mutual funds through the SIP (systematic investment plan) route to the tune of 35%. This has been further divided into four funds.
- 40% of my capital is invested in an equity portfolio of roughly 12 stocks. Long-term investments for me include mutual funds and an equity portfolio (5 years and beyond).
- Short-term initiatives will receive 25% of the budget.
The short-term strategies include a bunch of trading strategies such as –
- Momentum-based swing trades (futures)
- Overnight futures/options/stock trades
- Intraday trades
- Option writing
I make certain that I do not expose more than 35% of my total money to any single technique. To clarify, if I had Rs.500,000/- as my starting capital, here is how I would divide it:
- 35% of Rs.500,000/- i.e Rs.175,000/- goes to Mutual Funds
- 40% of Rs.500,000/- i.e Rs.200,000/- goes to equity portfolio
- 25% of Rs.500,000/- i.e Rs.125,000/- goes to short term trading
- 35% of Rs.125,000/- i.e Rs.43,750/- is the maximum I would allocate per trade
- Hence I will not be
So this self-mandated rule ensures that I do not expose more than 9% of my overall capital to any particular short-term strategies including option writing.
Instruments – I prefer running this strategy on liquid stocks and indices. Besides Nifty and Bank Nifty, I run this strategy on SBI, Infosys, Reliance, Tata Steel, Tata Motors, and TCS. I rarely venture outside this list.
So here’s what I’d advise you to do. Calculate the SD and mean for Nifty and Bank Nifty on the morning of August 21st (5 to 7 days before expiry). Find strikes that are one standard deviation away from the market price and write them digitally. Wait till the trade expires to see how it happens. If you have the necessary bandwidth, you can run this over all of the stocks I’ve highlighted. Perform this diligently for a few expiries before deploying funds.
Finally, as a typical caveat, the concepts mentioned here suit my risk-reward temperament, which may differ greatly from yours. Everything I’ve said here is based on my own personal trading experience, these are not standard practices.
I recommend that you take notice of these points, as well as understand your personal risk-reward temperament and calibrate your plan. Hopefully, the suggestions above may assist you in developing that orientation.
This is directly contradictory to the topic of this chapter, but I must recommend that you read Nassim Nicholas Taleb’s “Fooled by Randomness” at this point. The book forces you to evaluate and reconsider everything you do in marketplaces (and life in general). I believe that simply being conscious of what Taleb writes in his book, as well as the actions you do in markets, puts you in an entirely different orbit.
Volatility based stoploss
This is a departure from Options, and it would have been more appropriate in the futures trading module, but I believe we are in the appropriate position to examine it.
The first thing you should do before starting any trade is to choose the stop-loss (SL) price. The SL, as you may know, is a price threshold beyond which you will not take any further losses. For example, if you buy Nifty futures at 8300, you may set a stop-loss threshold of 8200; you will be risking 100 points on this trade. When the Nifty falls below 8200, you exit the trade and take a loss. The challenge is, however, how to determine the right stop-loss level.
Many traders follow a typical technique in which they keep a fixed % stop-loss. For example, on each transaction, a 2% stop-loss could be used. So, if you buy a stock at Rs.500, your stop-loss price is Rs.490, and your risk on this transaction is Rs.10 (2 percent of Rs.500). The issue with this method is the practice’s rigidity. It does not take into account the stock’s daily noise or volatility. For example, the nature of the stock could cause it to fluctuate by 2-3% on a daily basis. As a result, you may be correct about the direction of the transaction but still hit stop-loss.’ Keeping such tight stops will almost always be a mistake.
Estimating the stock’s volatility is an alternative and effective way for determining a stop-loss price. The daily ‘anticipated’ movement in the stock price is accounted for by volatility. The advantage of this technique is that the stock’s daily noise is taken into account. The volatility stop is crucial because it allows us to establish a stop at a price point that is outside of the stock’s regular expected volatility. As a result, a volatility SL provides us with the necessary rational exit if the transaction goes against us.
Let’s look at an example of how the volatility-based SL is implemented.
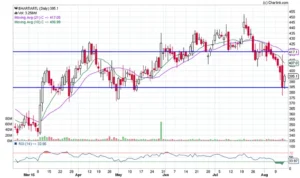
This is the chart of Airtel creating a bullish harami; those familiar with the pattern would recognise this as a chance to go long on the stock, using the previous day’s low (also support) as the stoploss. The immediate resistance would be the aim – both S&R sites are shown with a blue line. Assume you expect the trade to be completed during the next five trading sessions. The following are the trade specifics:
- Long @ 395
- Stop-loss @ 385
- Target @ 417
- Risk = 395 – 385 = 10 or about 2.5% below entry price
- Reward = 417 – 385 = 32 or about 8.1% above entry price
- Reward to Risk Ratio = 32/10 = 3.2 meaning for every 1 point risk, the expected reward is 3.2 point
From a risk-to-reward standpoint, this appears to be a smart trade. In fact, I consider any short-term transaction with a Reward to Risk Ratio of 1.5 to be a good trade. Everything, however, is dependent on the assumption that the stoploss of 385 is reasonable.
Let us run some numbers and delve a little more to see if this makes sense –
Step 1: Calculate Airtel’s daily volatility. I did the arithmetic, and the daily volatility is 1.8 percent.
Step 2: Convert daily volatility to volatility of the time period of interest. This is accomplished by multiplying the daily volatility by the square root of time. In our example, the predicted holding period is 5 days, hence the volatility is 1.8 percent *Sqrt (5). This equates to approximately 4.01 percent.
Step 3: Subtract 4.01 percent (5 day volatility) from the predicted entry price to calculate the stop-loss price. 379 = 395 – (4.01 percent of 395) According to the aforesaid calculation, Airtel can easily move from 395 to 379 in the next 5 days. This also implies that a stoploss of 385 can be readily overcome. So the stop loss for this trade must be a price point lower than 379, say 375, which is 20 points lower than the entry price of 395.
Step 4: With the updated SL, the RRR is 1.6 (32/20), which is still acceptable to me. As a result, I would be delighted to start the trade.
Note that if our predicted holding duration is 10 days, the volatility will be 1.6*sqrt(10), and so on.
The daily movement of stock prices is not taken into account with a fixed % stop-loss. There is a good risk that the trader places a premature stop-loss, well within the stock’s noise levels. This invariably results in the stop-loss being hit first, followed by the target.
Volatility-based stop-loss accounts for all daily predicted fluctuations in stock prices. As a result, if we use stock volatility to set our stop-loss, we are factoring in the noise component and so setting a more relevant stop loss.